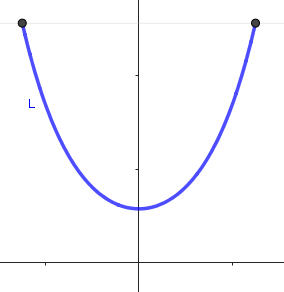

es \[f(x)=a·cosh\left(\dfrac{x}{a}\right), \ \ \ \left(-\frac{S}{2}<x<\frac{S}{2}\right)\]
siendo S la distancia entre los dos puntos de amarre de la cadena.
Para invertirla le cambiamos el signo
\[g(x)=-a·cosh\left(\dfrac{x}{a}\right)\]
Y para que los puntos de amarre queden fijos le sumamos
\[L=\displaystyle\int_{-x}^x \sqrt{1+f'(t)^2}\,dt\]
Derivando f(x):
\[f'(x)=a·senh\left(\dfrac{x}{a}\right)·\dfrac{1}{a}=senh\left(\dfrac{x}{a}\right)\]
Sustituyendo:
\[L=\displaystyle\int_{-x}^x \sqrt{1+sinh^2\left(\dfrac{t}{a}\right)}\,dt=\displaystyle\int_{-x}^x \sqrt{cosh^2\left(\dfrac{t}{a}\right)}\,dt=\displaystyle\int_{-x}^x cosh\left(\dfrac{t}{a}\right)\,dt=a·senh\left(\dfrac{t}{a}\right)\Biggr]_{-x}^x\]
Por Barrow:
\[L=a·senh\left(\dfrac{x}{a}\right)-a·senh\left(-\dfrac{x}{a}\right)\]
Como senh es impar,
\[L=2a·senh\left(\dfrac{x}{a}\right)\]
Si llamamos S = 2x (S es, entonces, la separación horizontal entre los dos exttremos del arco), tenemos:
\[L=2a·senh\left(\dfrac{S}{2a}\right)\]
Si damos por conocido el valor de L y buscamos el de a, nuestra ecuación queda como
\[L=2x·senh\left(\dfrac{S}{2x}\right)\]
Al tratrarse de una ecuación trascendente sin una solución explícita evidente, sustituimos el senh(x) por su polinomio de Taylor de orden 11
\[senh(x)\approx x +\dfrac{x³}{3!} + \dfrac{x⁵}{5!} + \dfrac{x⁷}{7!} + \dfrac{x⁹}{9!} + \dfrac{x¹¹}{11!}\]
y hacemos que Geogebra resuelva la ecuación polinómica resultante.
El resultado se puede ver en la construcción siguiente. El deslizador permite modificar la separación entre los dos extremos.