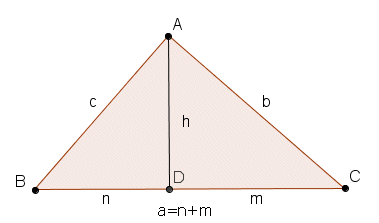
Sea ABC un triángulo rectángulo. Sea h la altura sobre la hipotenusa y sean m y n las proyecciones de los catetos sobre la hipotenusa: entonces se tiene que \(h^2=m·n\)

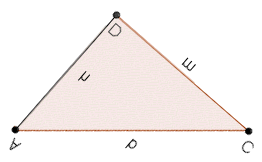
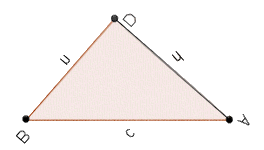
DEMOSTRACIÓN 1

El ángulo ABD y el ángulo DAC son iguales por ser ambos complementarios del ángulo BAD.

(Dibujo abajo ambos triángulos sin corregir la orientación de las letras para que se vea el movimiento.)

Por tanto, los triángulos BDA y ADC son semejantes, por lo que sus lados son prorporcionales.

Así: \[\dfrac{h}{n}=\dfrac{m}{h}\]

Multiplicando en cruz: \[h^2=m·n\]

DEMOSTRACIÓN 2

Esta demostración se basa en el teorema de Pitágoras.

\((m+n)^2=b^2+c^2\)       [1]

\(c^2=h^2+n^2\)              [2]

\(b^2=h^2+m^2\)               [3]

Sustituyendo [2] y [3] en [1]:

\((m+n)^2=h^2+m^2+h^2+n^2\) 

Desarrollando:

\(m^2+n^2+2mn=h^2+m^2+h^2+n^2\)

y, simplificando:

\(2mn=2h^2\)

y, por tanto:

\(h^2=m·n\)