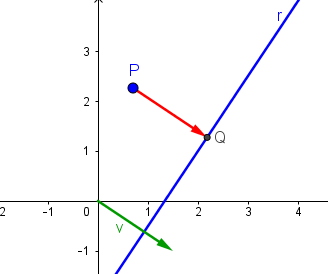
Sean la recta \(r: Ax+By+C=0\) y el punto \(P=(p_1,p_2)\). Vamos a calcular la distancia de P a r.

Sea Q la proyección de P sobre r. Entonces \(d(P,r)=d(P,Q)=|\vec{PQ}|\)

Sea el vector \(\vec{v}=(A,B)\), que es perpendicular a \(r\).

Por definición, \(\vec{PQ}·\vec{v}=|\vec{PQ}|·|\vec{v}|· cos(\vec{PQ},\vec{v}) \)

Como \(\vec{v}\) y \(\vec{PQ}\) son paralelos, \(cos(\vec{PQ},\vec{v})=\pm 1\)

Tomando valor absoluto: \(|\vec{PQ}·\vec{v}|=|\vec{PQ}|·|\vec{v}|\)

Despejando: \(|\vec{PQ}|=\dfrac{|\vec{PQ}·\vec{v}|}{|\vec{v}|}\)

Suponiendo un sistema de referencia ortonormal:

\(\vec{PQ}·\vec{v}=(q_1-p_1)A+(q_2-p_2)B=q_1A+q_2B-p_1A-p_2B\)

Como \(Q \in r \Rightarrow q_1A+q_2B+C=0\Rightarrow q_1A+q_2B=-C\)

Así:

\(|\vec{PQ}·\vec{v}|=|(q_1-p_1)A+(q_2-p_2)B|=|-p_1A-p_2B-C|=|p_1A+p_2B+C|\)

Sustituyendo: \(d(P,r)=\dfrac{|Ap_1+Bp_2+C|}{|\sqrt{A^2+B^2}|}\)