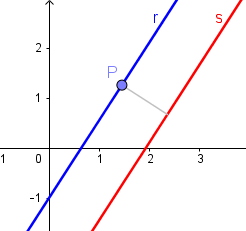
Sean las rectas paralelas \(r: Ax+By+C=0\) y \(s: Ax+By+C'=0\).

Sea P un punto de r. Entonces: \(d(r,s)=d(P,s)\)

Aplicando la fórmula deducida en distancia punto-recta, \(d(P,s)=\dfrac{|Ap_1+Bp_2+C'|}{|\sqrt{A^2+B^2}|}\)

Pero, como \(P\in r\), se tiene que \(Ap_1+Bp_2+C=0\)

Despejando: \(Ap_1+Bp_2=-C\)

Por tanto, \(d(P,s)=\dfrac{|C'-C|}{|\sqrt{A^2+B^2}|}\)