| Epsiclas | ||
Resumen trigonometría 4º ESO |
||
Razones trigonométricas del ángulo agudoEn un triángulo retángulo se definen las razones trigonométricas de un ángulo agudo \(\alpha\) de la siguiente manera:
En la figura: \({\rm sen}\alpha=\dfrac{b}{a}\); \({\rm cos}\alpha=\dfrac{c}{a}\); \({\rm tg}\alpha=\dfrac{b}{c}\)
|
| \[\alpha\] | 0º | 30º | 45º | 60º | 90º |
| \[{\rm sen\alpha}\] | \[\frac{\sqrt0}{2}=0\] | \[\frac{\sqrt1}{2}=\frac{1}{2}\] | \[\frac{\sqrt2}{2}\] | \[\frac{\sqrt3}{2}\] | \[\frac{\sqrt4}{2}=1\] |
| \[{\rm cos\alpha}\] | \[\frac{\sqrt4}{2}=1\] | \[\frac{\sqrt3}{2}\] | \[\frac{\sqrt2}{2}\] | \[\frac{\sqrt1}{2}=\frac{1}{2}\] | \[\frac{\sqrt0}{2}=0\] |
| \[{\rm tg\alpha}\] | 0 | \[\frac{\sqrt3}{3}\] | 1 | \[\sqrt3\] | \[\infty\] |
Observese que la segunda fila se deduce aplicando la relación existente entre las razones de los ángulos complementarios y la tercera de calcular la tangente como el cociente entre el seno y el coseno.
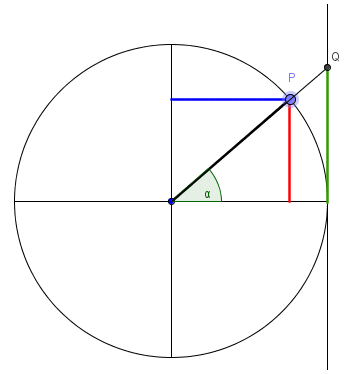
Reducción al primer cuadrante
Si \(\alpha\) pertenece al segundo cuadrante, se toma \(\beta=180º-\alpha\)
Si \(\alpha\) pertenece al tercer cuadrante, se toma \(\beta=\alpha-180º\)
Si \(\alpha\) pertenece al cuarto cuadrante, se toma \(\beta=360º-\alpha\)
Las relaciones anteriores se deducen fácilmente a partir de la circunferencia goniométrica.
 Teoremas del seno y del coseno
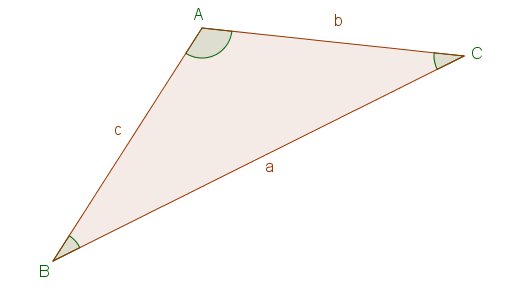
Teoremas del seno y del coseno
Teorema del seno
\(\dfrac{a}{sen A}=\dfrac{b}{sen B}=\dfrac{c}{sen C}\)
Teorema del coseno
\(c^2=a^2+b^2-2ab cosC\)
Inversas numéricas
\({\rm cosec}\alpha=\dfrac{1}{\rm sen\alpha}\)
\({\rm sec}\alpha=\dfrac{1}{\rm cos\alpha}\)
\({\rm cotg}\alpha=\dfrac{1}{\rm tg\alpha}\)
Inversas funcionales
La calculadora tiene funciones que, dado un valor, proporcionan uno de los ángulos cuyo seno, coseno o tangente corresponden a dicho valor. Hay que tener en cuenta el cuadrante para decidir si el ángulo proporcionado es el buscado o no.
\({\rm arcsen}x={\rm sen}^ {-1}x\)
\({\rm arccos}x={\rm cos}^ {-1}x\)
\({\rm arctg}x={\rm tg}^ {-1}x\)
| Aquí puedes hacer tus comentarios |
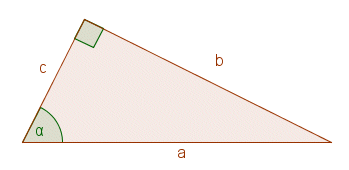 \({\rm sen}\alpha=\dfrac{cateto\ \ opuesto}{hipotenusa}\)
\({\rm sen}\alpha=\dfrac{cateto\ \ opuesto}{hipotenusa}\)